Publications
Journal articles
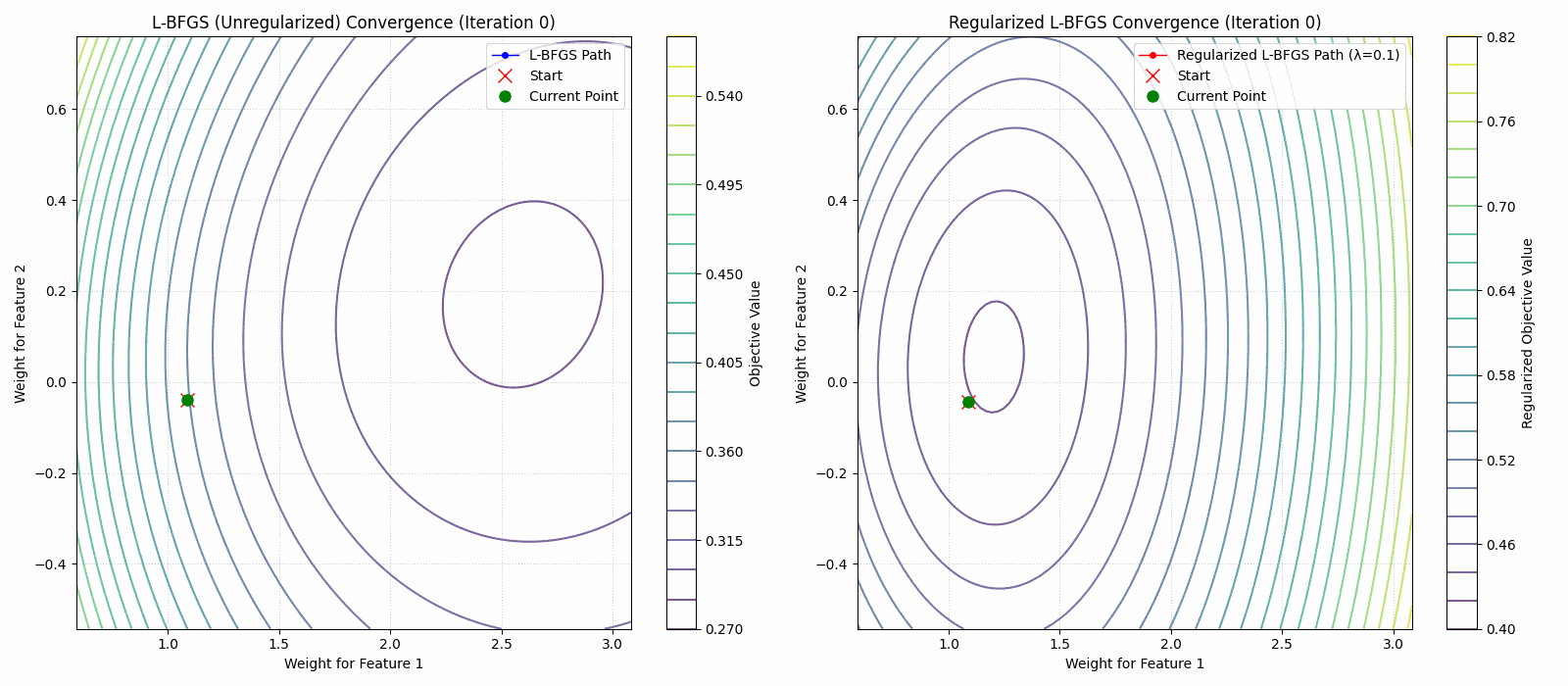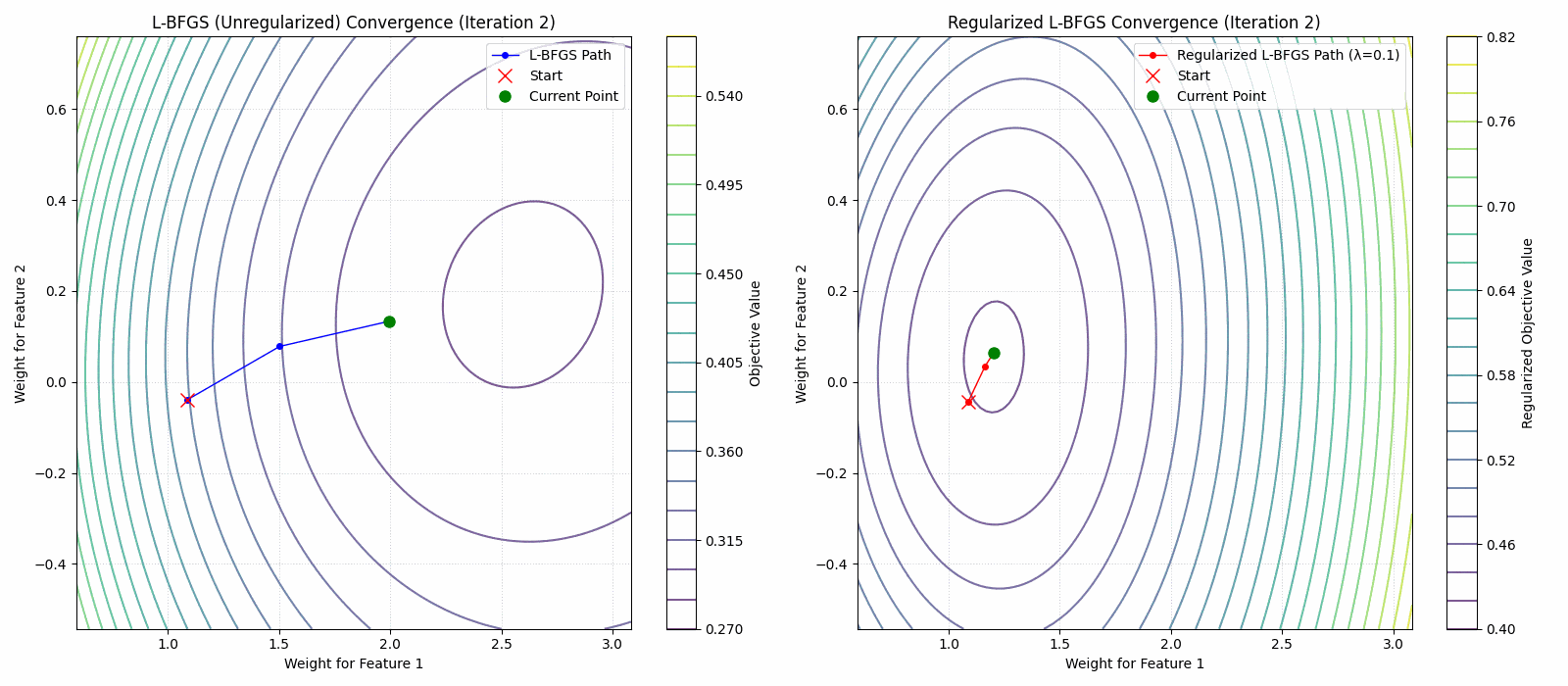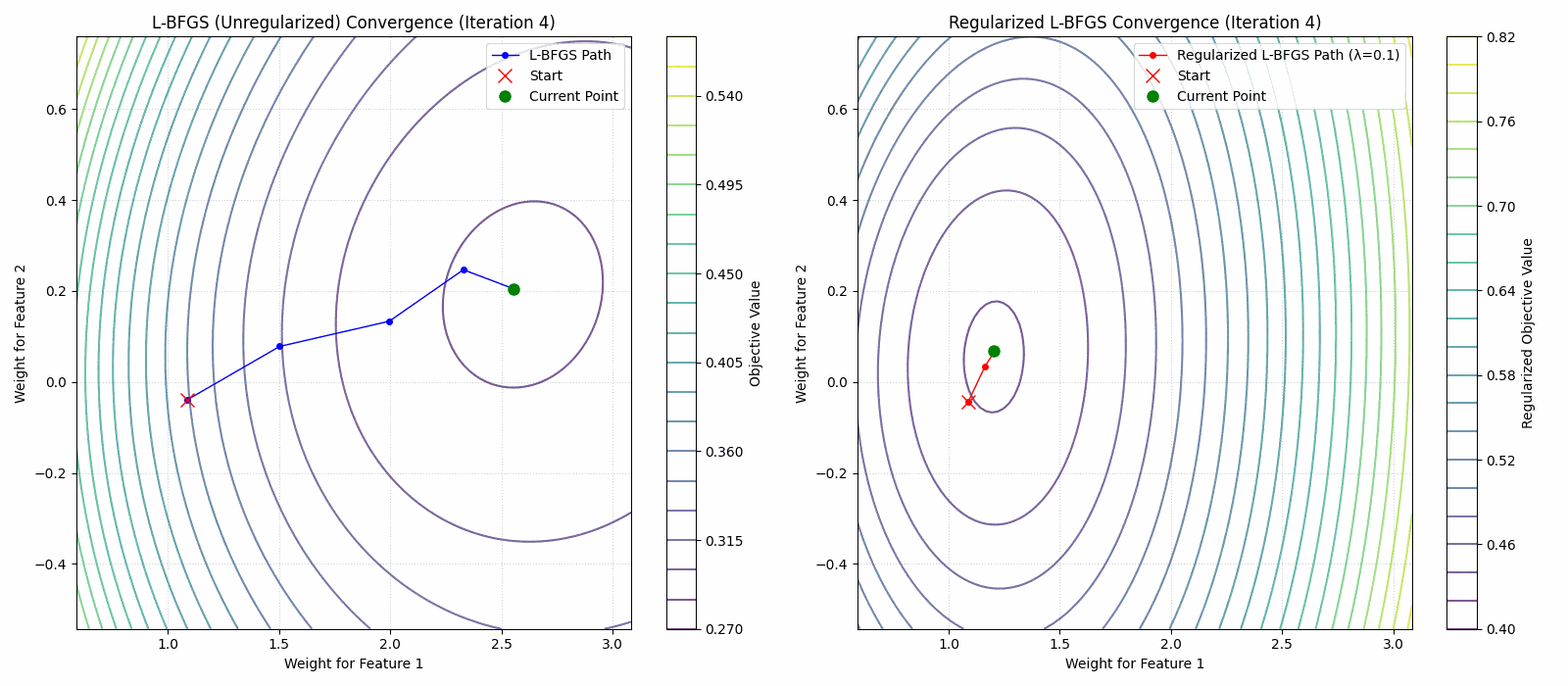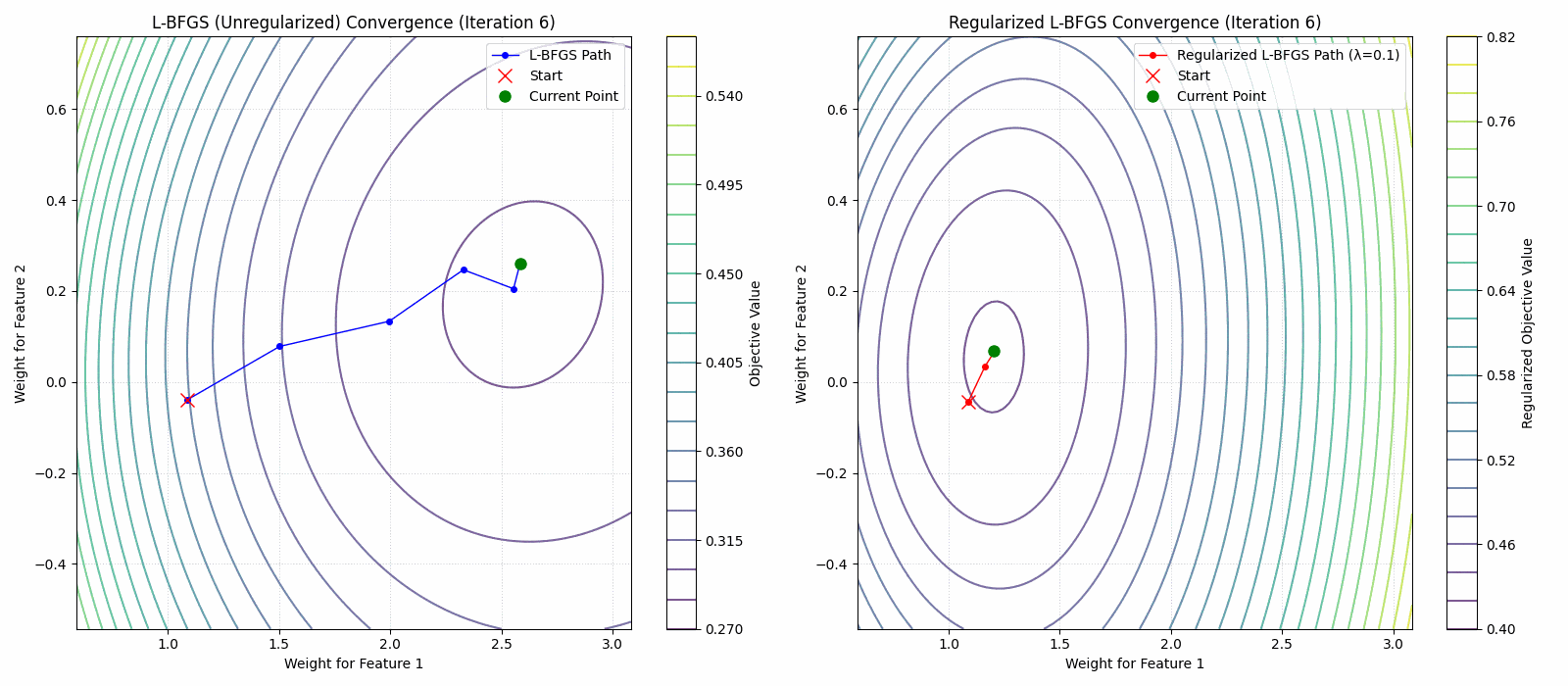
- A regularized limited memory BFGS method for large-scale unconstrained optimization and its efficient implementationsComputational Optimization and Applications, 2022The limited memory BFGS (L-BFGS) method is one of the popular methods for solving large-scale unconstrained optimization. Since the standard L-BFGS method uses a line search to guarantee its global convergence, it sometimes requires a large number of function evaluations. To overcome the difficulty, we propose a new L-BFGS with a certain regularization technique. We show its global convergence under the usual assumptions. In order to make the method more robust and efficient, we also extend it with several techniques such as the nonmonotone technique and simultaneous use of the Wolfe line search. Finally, we present some numerical results for test problems in CUTEst, which show that the proposed method is robust in terms of solving more problems.
- A stochastic variance reduced gradient using Barzilai-Borwein techniques as second order informationJournal of Industrial and Management Optimization, 2022In this paper, we consider to improve the stochastic variance reduce gradient (SVRG) method via incorporating the curvature information of the objective function. We propose to reduce the variance of stochastic gradients using the computationally efficient Barzilai-Borwein (BB) method by incorporating it into the SVRG. We also incorporate a BB-step size as its variant. We prove its linear convergence theorem that works not only for the proposed method but also for the other existing variants of SVRG with second-order information. We conduct the numerical experiments on the benchmark datasets and show that the proposed method with constant step size performs better than the existing variance reduced methods for some test problems.
Preprint
- arXiv
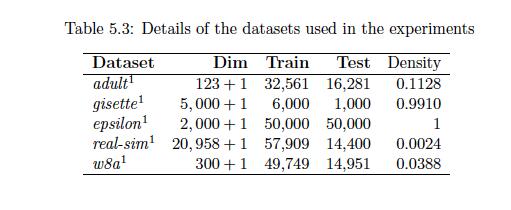
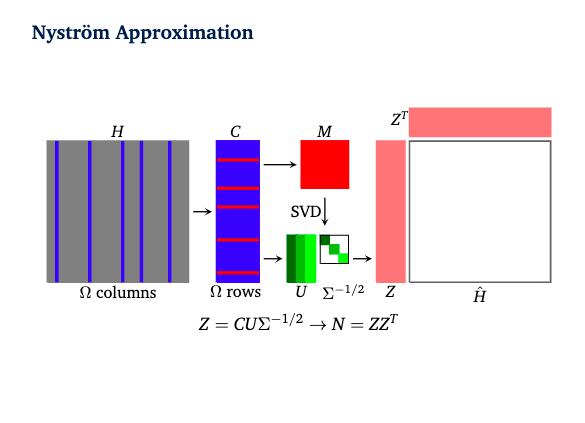
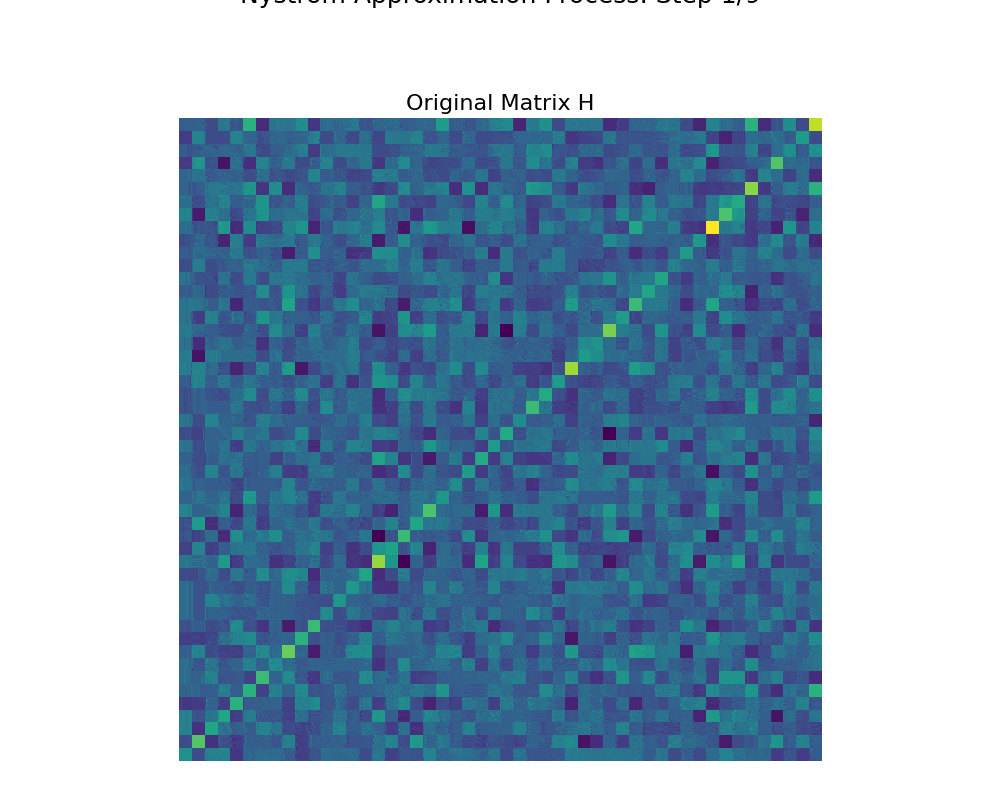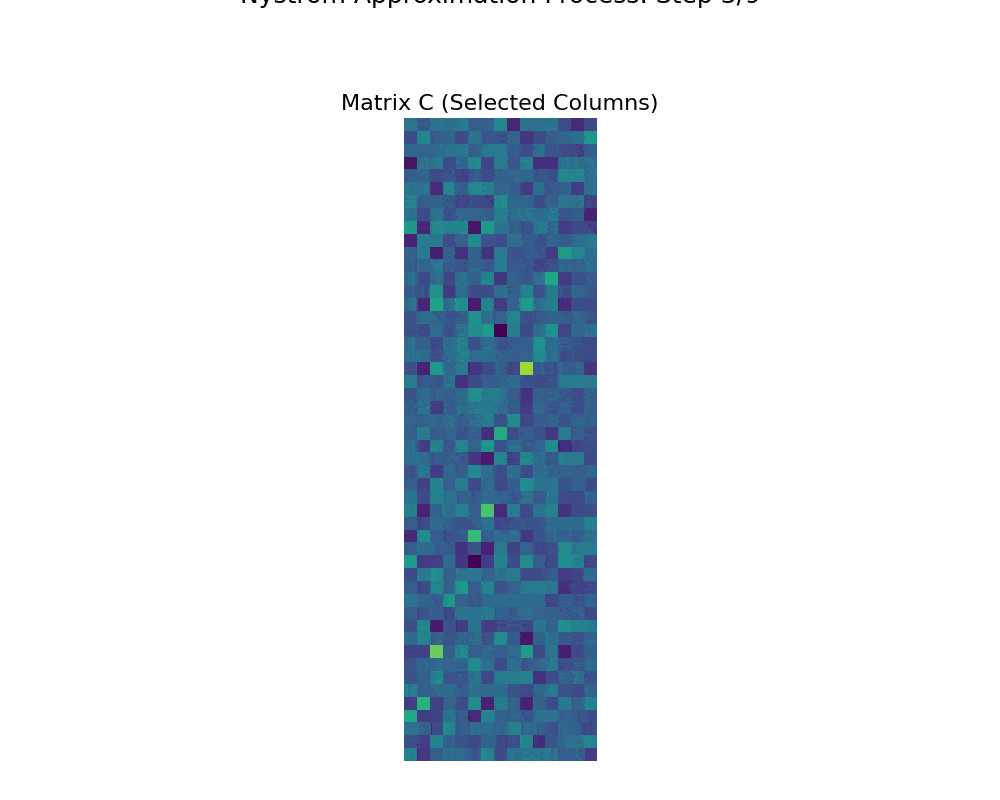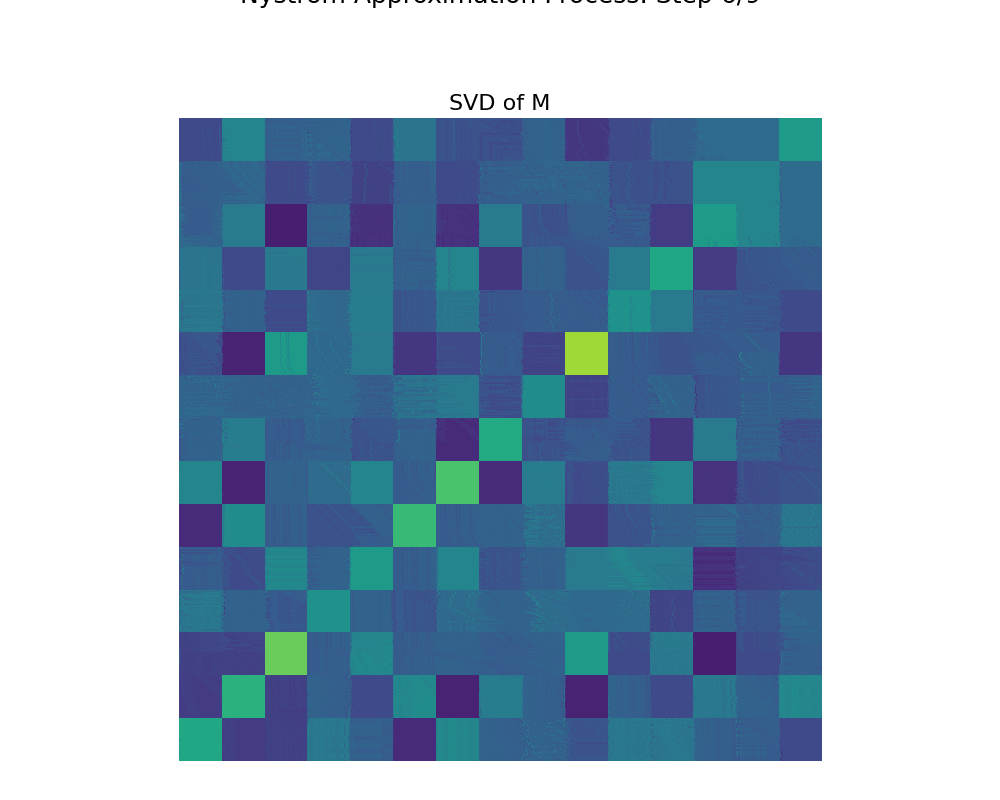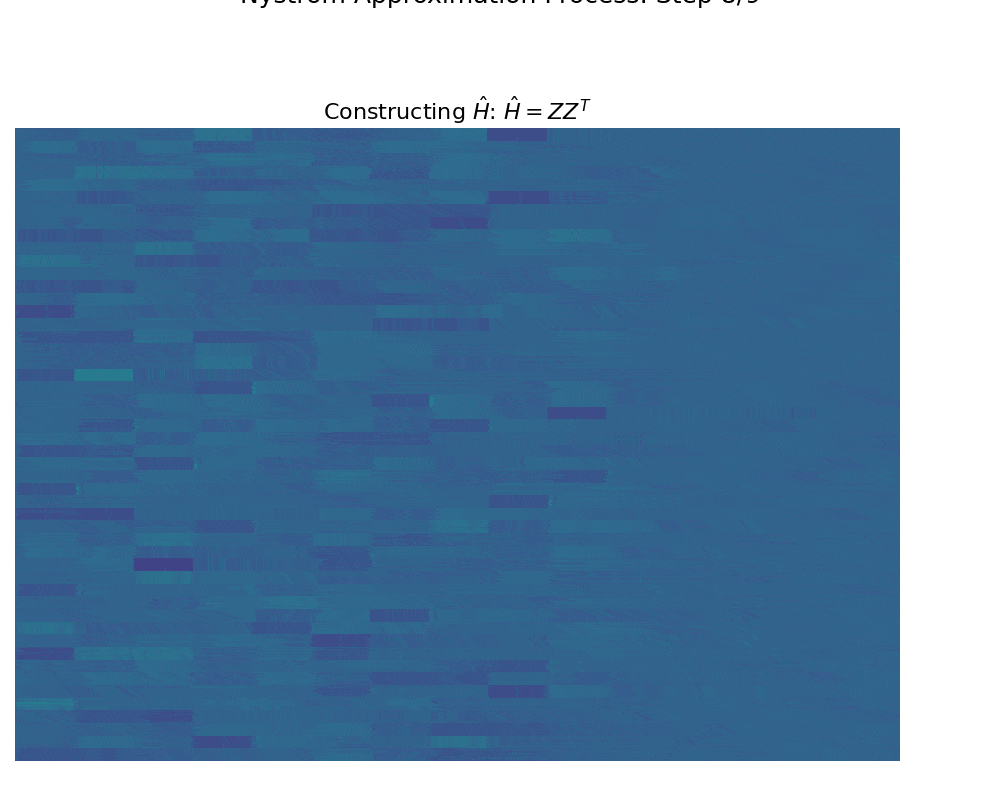Nys-curve: Nyström-approximated curvature for stochastic optimization2021The quasi-Newton methods generally provide curvature information by approximating the Hessian using the secant equation. However, the secant equation becomes insipid in approximating the Newton step owing to its use of the first-order derivatives. In this study, we propose an approximate Newton step-based stochastic optimization algorithm for large-scale empirical risk minimization of convex functions with linear convergence rates. Specifically, we compute a partial column Hessian of size (d×k) with k <d randomly selected variables, then use the \textitNyström method to better approximate the full Hessian matrix. To further reduce the computational complexity per iteration, we directly compute the update step (\deltaw) without computing and storing the full Hessian or its inverse. Furthermore, to address large-scale scenarios in which even computing a partial Hessian may require significant time, we used distribution-preserving (DP) sub-sampling to compute a partial Hessian. The DP sub-sampling generates p sub-samples with similar first and second-order distribution statistics and selects a single sub-sample at each epoch in a round-robin manner to compute the partial Hessian. We integrate our approximated Hessian with stochastic gradient descent and stochastic variance-reduced gradients to solve the logistic regression problem. The numerical experiments show that the proposed approach was able to obtain a better approximation of Newton’s method with performance competitive with the state-of-the-art first-order and the stochastic quasi-Newton methods. - ResearchGate
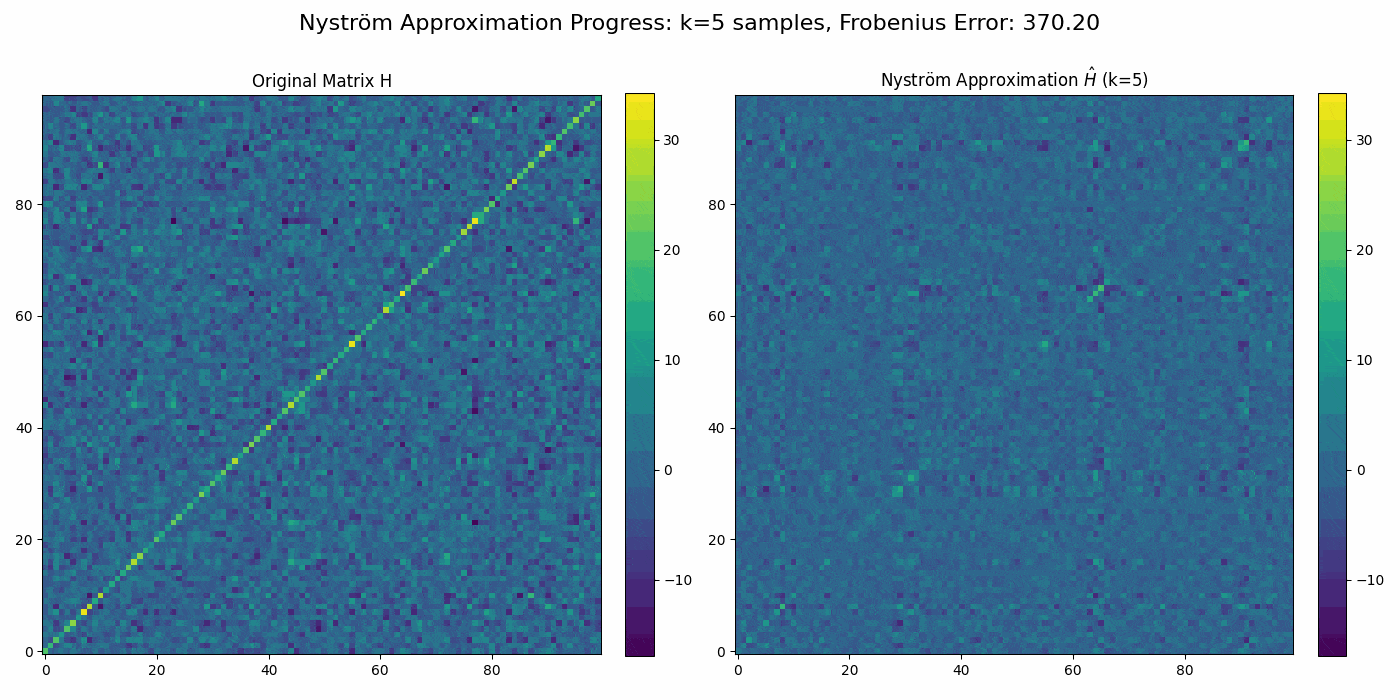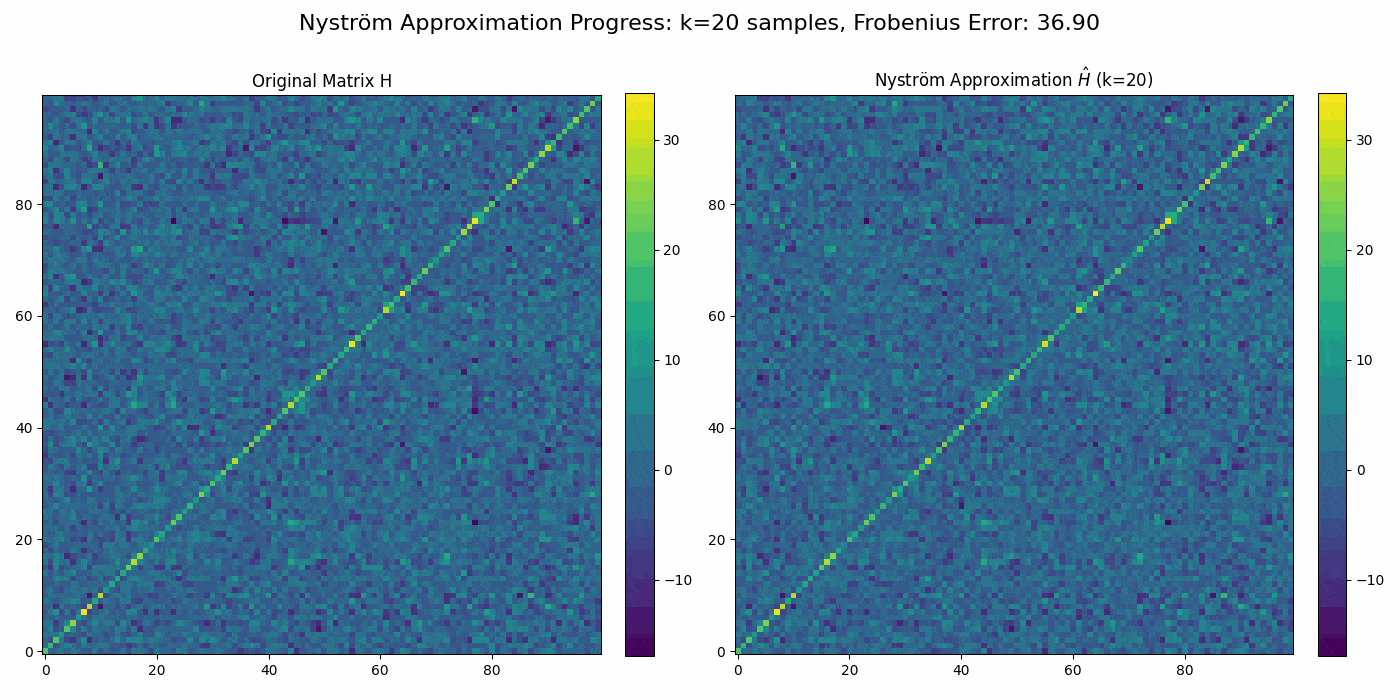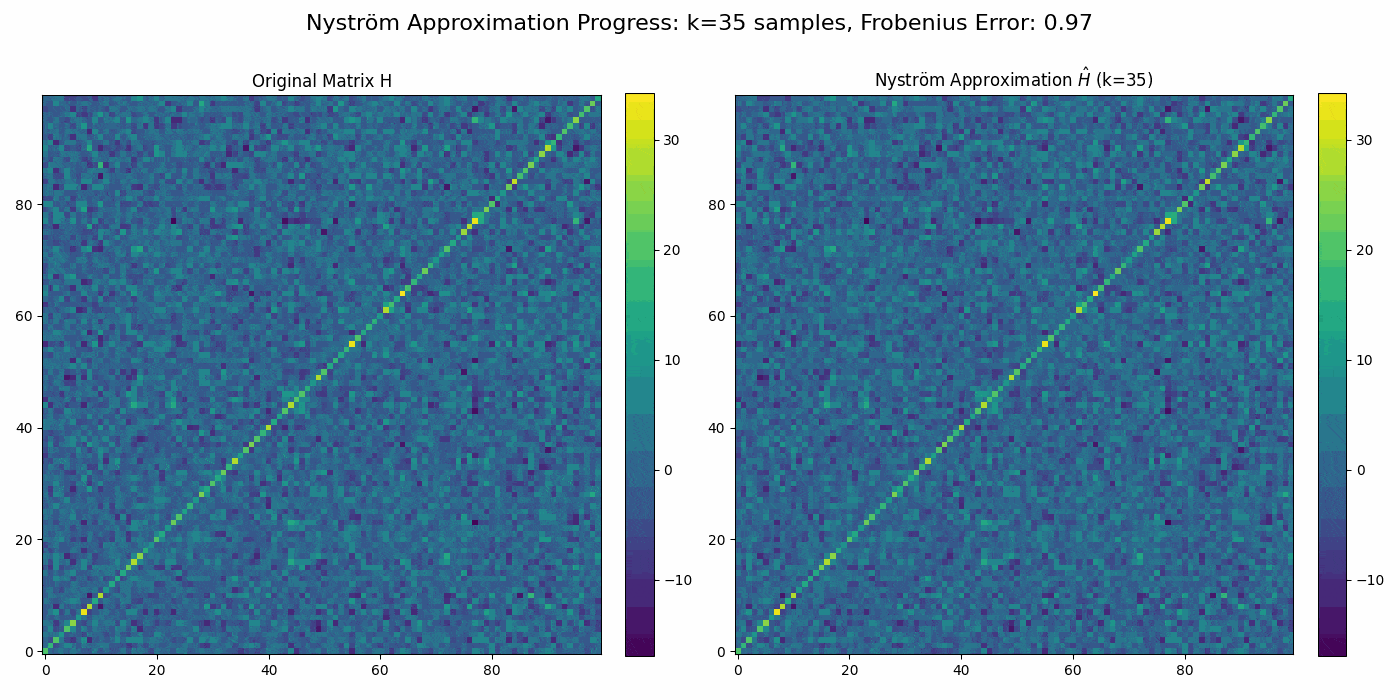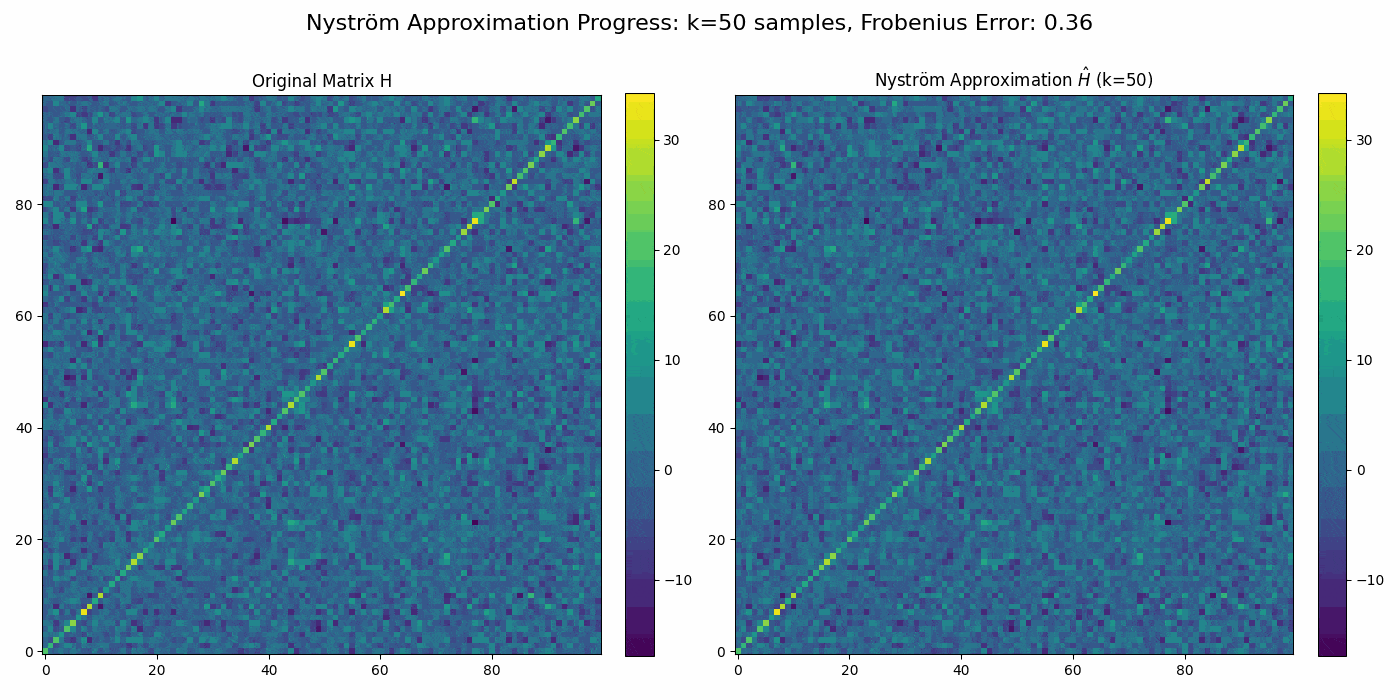Regularized Nyström method for Large-Scale Unconstrained Non-Convex Optimization2024We propose a quasi-Newton type regularized Nyström method for solving unconstrained large scale non-convex optimization problem with high-dimensional feature spaces. We focus on l2-regularized objective function. To efficiently approximate the Hessian, we employ a regularized Nystrom method to approximate Hessian. However, the Hessian of non-convex function may produce negative eigenvalues. We confront the issue of negative eigenvalue via incorporating the regularized parameter to obtain positive definite matrix and the descent direction, resulting in to the regulazied fixed-rank Nystrom approximation. This fixed-rank approximation offers flexibility in rank selection through random column sampling, enhancing computational efficiency. Complementing this, we employ backtracking line search to ascertain suitable step sizes, utilizing partial Hessian information to approximate the full Hessian matrix. We establish global convergence under standard assumptions and provide a comprehensive analysis of the global complexity. Finally, we demonstrate numerical experiments to show the robustness and efficiency of the proposed method by comparing it with existing methods.
Theses
- Master ThesisHasse-Minkowski principle for Quadratic forms over Q2016This master’s thesis covers the Hasse–Minkowski theorem, a central theorem in number theory. The theorem states that two quadratic forms over a number field are equivalent if and only if they are equivalent at all completions of the number field. The paper looks into the proof of this theorem, in relation to quadratic forms over the rationals. It addresses the local-global principle when exploring equivalence, emphasizing the relationship between local properties at different places (like real and p-adic completions) and global properties over the rationals. The thesis reinforces what we understand about quadratic forms, and illustrates how the Hasse–Minkowski principle and theorem relate to algebraic number theory as a whole.