Reg-Nyström Optimization for Machine Learning
Hessian Sketching for Scalable ML Optimization is a second-order optimization framework that combines Nyström-based Hessian approximation with adaptive regularization to enable fast, stable training of large-scale machine learning models
NysReg-Gradient: Regularized Nyström-Gradient for Large-Scale Unconstrained Optimization and its Application
We develop a regularized Nyström method for solving unconstrained optimization problems with high-dimensional feature spaces. Our method leverages the actual Hessian information and proposes a balanced approach by introducing the regularized Nyström approximation. We integrate approximated Hessian with gradient descent and stochastic gradient descent. The numerical experiments demonstrate that it notably outperforms the randomized subspace Newton and the approximation of Newton-sketch, showing considerable advancements in optimization with high-dimensional feature space.
Table of Contents
- Problem Statement and Motivation
- Core Methodology
- Stochastic Variant
- Experimental Results
- Theoretical Contributions
- Real-World Application
- Significance and Impact
- Relevant Citations
Problem Statement and Motivation
Large-scale optimization problems are ubiquitous in machine learning, where the challenge lies in balancing computational efficiency with convergence speed. First-order methods like gradient descent are computationally cheap but suffer from slow convergence, particularly on ill-conditioned problems. Second-order methods like Newton’s method converge faster but require computing and inverting the Hessian matrix, which becomes prohibitively expensive for high-dimensional problems with a cost of $O(d^3)$.
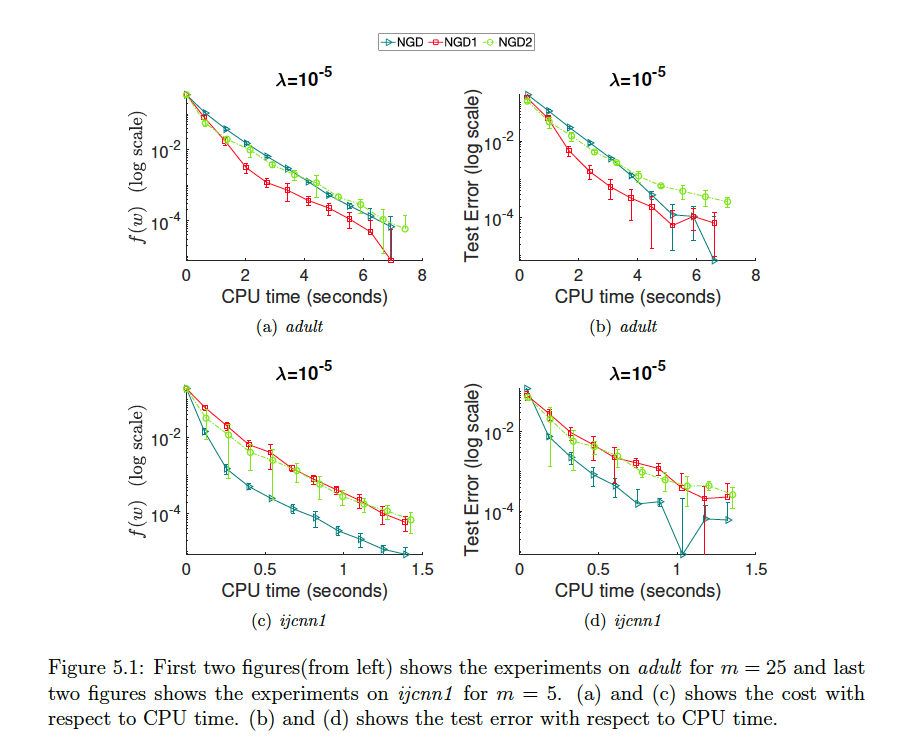
Performance comparison of NGD variants (NGD, NGD1, NGD2) on adult and ijcnn1 datasets, showing training cost and test error over CPU time.
This paper introduces NysReg-Gradient (NGD), a second-order optimization method that uses regularized Nyström approximation to efficiently approximate the Hessian matrix. The method aims to capture the benefits of second-order information while maintaining computational tractability for large-scale problems.
Core Methodology
Nyström Approximation Foundation
The Nyström method approximates a symmetric positive semi-definite matrix by sampling a subset of its columns. For a Hessian matrix $H \in \mathbb{R}^{d \times d}$, the method samples $m$ columns to form matrix $C \in \mathbb{R}^{d \times m}$, and constructs an intersection matrix $M \in \mathbb{R}^{m \times m}$ from the corresponding rows and columns. The Nyström approximation is:
\[N_k = C M_k^+ C^T\]where $M_k^+$ is the pseudo-inverse of the best rank-$k$ approximation of $M$, with $k \leq m$.
Regularized Update Rule
The NysReg-Gradient update follows the form:
\[w_{t+1} = w_t - \eta_t (N_t + \rho_t I)^{-1} \nabla f(w_t)\]The key innovation is the adaptive regularization parameter:
\[\rho_t = c_1 \|\nabla f(w_t)\|^\gamma\]where $c_1 > 0$ and $\gamma$ determines the regularization strength. The paper explores three variants:
- NGD: $\gamma = 1/2$
- NGD1: $\gamma = 1$
- NGD2: $\gamma = 2$
This gradient-dependent regularization ensures the matrix $(N_t + \rho_t I)$ remains non-singular and provides theoretical guarantees for convergence.
Computational Efficiency
The method achieves efficiency through the Sherman-Morrison-Woodbury identity, avoiding direct inversion of the $d \times d$ matrix $(N_t + \rho_t I)$. Instead, it computes:
\[(N_t + \rho_t I)^{-1} = \frac{1}{\rho_t}I - \frac{1}{\rho_t^2} Z_t (I_k + \frac{1}{\rho_t} Z_t^T Z_t)^{-1} Z_t^T\]where $Z_t$ is derived from the SVD of the sampled matrix $C_t$. This reduces the per-iteration complexity to $O(dm)$, where $m \ll d$, making it practical for high-dimensional problems.
Stochastic Variant
For large datasets, the paper introduces NysReg-Stochastic Gradient Descent (NSGD). This variant uses mini-batch stochastic gradients at each iteration while updating the Nyström approximation less frequently (e.g., once per epoch). The regularization parameter $\rho_\tau$ is computed based on the stochastic gradient norm from the previous epoch, balancing computational efficiency with approximation quality.
Experimental Results
Sketch Size Analysis
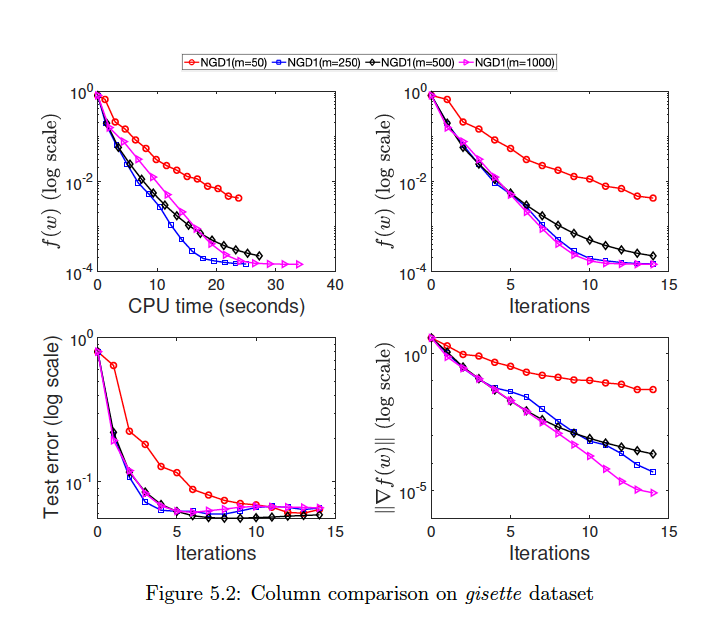
Effect of sketch size (m) on NGD1 performance across different datasets, showing training cost, iterations, test error, and gradient norm.
The experiments demonstrate that relatively small sketch sizes are sufficient for good performance. For dense datasets like gisette, using only 5% of the dimension as sketch size achieves competitive results. Sparse datasets like w8a require larger sketch sizes (15-20% of dimension) to capture sufficient Hessian information.
Theoretical Contributions
The paper provides convergence analysis showing that NGD achieves superlinear convergence under appropriate conditions. The authors prove bounds on the difference between NGD’s direction and Newton’s direction, establishing theoretical foundations for the method’s effectiveness.
The connection to Newton Sketch is particularly insightful. The paper shows that Nyström approximation can be expressed as $X^T U_k U_k^T X + \rho I$, where $U_k$ is a natural orthogonal matrix derived from data structure, contrasting with Newton Sketch’s random embedding matrix. This suggests Nyström may provide more accurate approximations, especially for small sketch sizes.
Real-World Application

Sample MRI images from the brain tumor detection dataset, showing various tumor types and normal brain tissue.
Total 253 images. 1000 dimension, 177 train size 76 test size, with positive cases: 46 and negative cases: 30 x_mri: [253×1000 single] x_test: [76×1000 single] x_train: [177×1000 single] y_test: [76×1 double] y_train: [177×1 double]
The method’s practical utility is demonstrated through a brain tumor detection application using MRI images. NGD variants achieve competitive performance in fine-tuning pre-trained deep networks for medical image classification, showing particular strength in limited-data scenarios where stable training is crucial.
Confusion Matrix Table (MRI Dataset)
| Method | TP | TN | FP | FN |
|---|---|---|---|---|
| NEWTON | 40 | 25 | 5 | 6 |
| GD | 30 | 27 | 3 | 16 |
| LBFGS | 39 | 26 | 4 | 7 |
| NGD | 39 | 28 | 2 | 7 |
| NGD1 | 39 | 26 | 4 | 7 |
| NGD2 | 39 | 26 | 4 | 7 |
| NSGD | 36 | 26 | 4 | 10 |
Metric Comparison Table (MRI Dataset)
| Method | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| NEWTON | 0.855263 | 0.888889 | 0.869565 | 0.879121 |
| GD | 0.750000 | 0.909091 | 0.652174 | 0.759494 |
| LBFGS | 0.855263 | 0.906977 | 0.847826 | 0.876404 |
| NGD | 0.881579 | 0.951220 | 0.847826 | 0.896552 |
| NGD1 | 0.855263 | 0.906977 | 0.847826 | 0.876404 |
| NGD2 | 0.855263 | 0.906977 | 0.847826 | 0.876404 |
| NSGD | 0.815789 | 0.900000 | 0.782609 | 0.837209 |
Significance and Impact
NysReg-Gradient represents a meaningful advance in bridging the gap between first-order and second-order optimization methods. Its adaptive regularization strategy and efficient computation make it particularly suitable for high-dimensional machine learning problems. The method’s versatility across different problem types—from strongly convex functions to complex deep learning models—demonstrates its broad applicability.
The theoretical analysis provides solid foundations, while extensive empirical validation across multiple domains establishes its practical value. The connection to existing methods like Newton Sketch provides valuable insights into the relative advantages of different Hessian approximation strategies, contributing to the broader understanding of second-order optimization techniques in machine learning.
Relevant Citations
- On the nyström method for approximating a gram matrix for improved kernel-based learning
- Petros Drineas and Michael W. Mahoney. Journal of Machine Learning Research, 6:2153–2175, 2005.
- This is the foundational paper for the Nyström approximation, which is the core technique used by the main paper to approximate the Hessian matrix.
- RSN: Randomized subspace newton
- Robert Gower, Dmitry Kovalev, Felix Lieder, and Peter Richtárik. Advances in Neural Information Processing Systems, 32, 2019.
- This paper introduces the Randomized Subspace Newton (RSN) method, a key state-of-the-art competitor.
- Newton sketch: A near linear-time optimization algorithm with linear-quadratic convergence
- Mert Pilanci and Martin J Wainwright. SIAM Journal on Optimization, 27(1):205–245, 2017.
- This work introduces the Newton sketch algorithm, another primary competitor in second-order optimization.
- Convergence properties of the regularized newton method for the unconstrained nonconvex optimization
- Kenji Ueda and Nobuo Yamashita. Applied Mathematics and Optimization, 62:27–46, 2010.
- This citation provides the direct inspiration for the regularization strategy used in the proposed ‘NysReg-Gradient’ method.