SVRG-2BB: Accelerating Large-Scale Machine Learning with Barzilai-Borwein Optimization

This project showcases my work on enhancing Stochastic Variance Reduced Gradient (SVRG) techniques by incorporating Barzilai-Borwein (BB) approximation for adaptive step-size selection. My goal was to significantly improve the convergence speed of gradient-based optimizers on large-scale convex machine learning problems, specifically L2-regularized logistic regression and support vector machines (SVMs).

📌 The Challenge: Gradient Noise in Large-Scale ML

In the realm of large-scale machine learning, gradient noise is a primary obstacle to efficient model training. While mini-batch or stochastic gradient descent (SGD) offers essential scalability for millions of data points, it often comes at the cost of high variance in updates, leading to noticeably slower convergence. This project directly addresses this challenge.

In vanilla SGD, the update direction is inherently noisy, causing updates to fluctuate considerably around the true gradient. This inherent noise can severely impede convergence, particularly as datasets scale up.

SVRG (Stochastic Variance Reduced Gradient) offers a powerful mitigation strategy. It introduces a control variate—anchoring noisy stochastic gradients to more accurate full-gradient snapshots taken periodically. This anchoring reduces gradient variance, enabling faster and more stable optimization.

However, further refinements are necessary to unlock the full potential of these methods in large-scale settings.

📈 My Solution: SVRG-2BB - Blending Variance Reduction with Second-Order Insight for Scalability

While SVRG effectively reduces variance, I found that performance can be further enhanced by strategically incorporating curvature information without computing full Hessian matrices. This is where the Barzilai-Borwein (BB) method proves invaluable.

BB is a step-size heuristic, derived from quasi-Newton methods, that efficiently estimates curvature.

Key Enhancements with SVRG-2BB:

Integrated BB into the core SVRG structure to achieve superior acceleration.
Dynamically adapted BB-approximated step sizes using historical gradient information within each epoch.
Preserved and enhanced SVRG’s variance-reduction structure to achieve synergy between variance control and second-order insight.

The result is faster, more stable convergence, especially on ill-conditioned, real-world, large-scale datasets.

🧪 Problem Formulations

This project tackles two fundamental machine learning optimization problems:

1. L2-Regularized Logistic Regression:

\[\min_w F(w) = \frac{1}{n} \sum_{i=1}^n \log(1 + \exp(-b_i a_i^T w)) + \frac{\lambda}{2} \|w\|^2\]

2. L2-Squared Support Vector Machine (SVM):

\[\min_w F(w) = \frac{1}{2n} \sum_{i=1}^n (\max(0, 1 - b_i a_i^T w))^2 + \frac{\lambda}{2} \|w\|^2\]

Where:

$a_i \in \mathbb{R}^d$: Feature vector
$b_i \in { \pm 1 }$: Binary label
$\lambda$: L2 regularization parameter

📁 Repository Structure

SVRG2BB/
├── SGD_lib/                    # Utility tools for learning rate, epochs, etc.
├── SVRG_BB/                    # Main repo for SVRG-2BB proposed method
│   ├── data/w8a.m              # Datasets (MAT files - eg. w8a.mat) and data loaders(w8a.m)
│   ├── Results_2022/           # Results from 2022 experiments
│   ├── Results_July2022/       # Latest experiment results
│   ├── BB_optimizers/bb_solvers/ # Core implementations of SVRG-BB methods
│   └── Problem/                # Loss functions, gradients, BB updates
├── Figures/
│   ├── adult/
│   ├── w8a/
│   ├── covtype/
│   ├── gisette/
│   ├── mnist38/
│   ├── ijcnn/
│   └── Figure_M1_M4/
├──SVRG_NUMERICAL_EXP.m    # Main experiment script
└── README.md

🚀 Key Features & My Implementation Highlights

Core SVRG Variants: Implemented SVRG, SVRG-2BB, and SVRG-2BBS in MATLAB.
Modular Design: Easy swapping of objectives and optimizers for flexibility.
Dataset Support: Benchmarks include Adult, W8A, Covtype, Gisette, Ijcnn, and Mnist.
Visualization Tools: Automatic plotting of:
- Optimality gap (vs. epoch / CPU time)
- Gradient variance (vs. epoch)

▶️ How to Run

First of all add the whole folder in MATLAB path.
Launch MATLAB and navigate to the experiment file:
```
 cd SVRG2BB/
```
Run the experiments:
```
 SVRG_NUMERICAL_EXP();
```
Generate performance plots:
```
 cd ../Figures/
 ploter();
```

Plots are saved as .eps files in dataset-specific folders under Figures/.

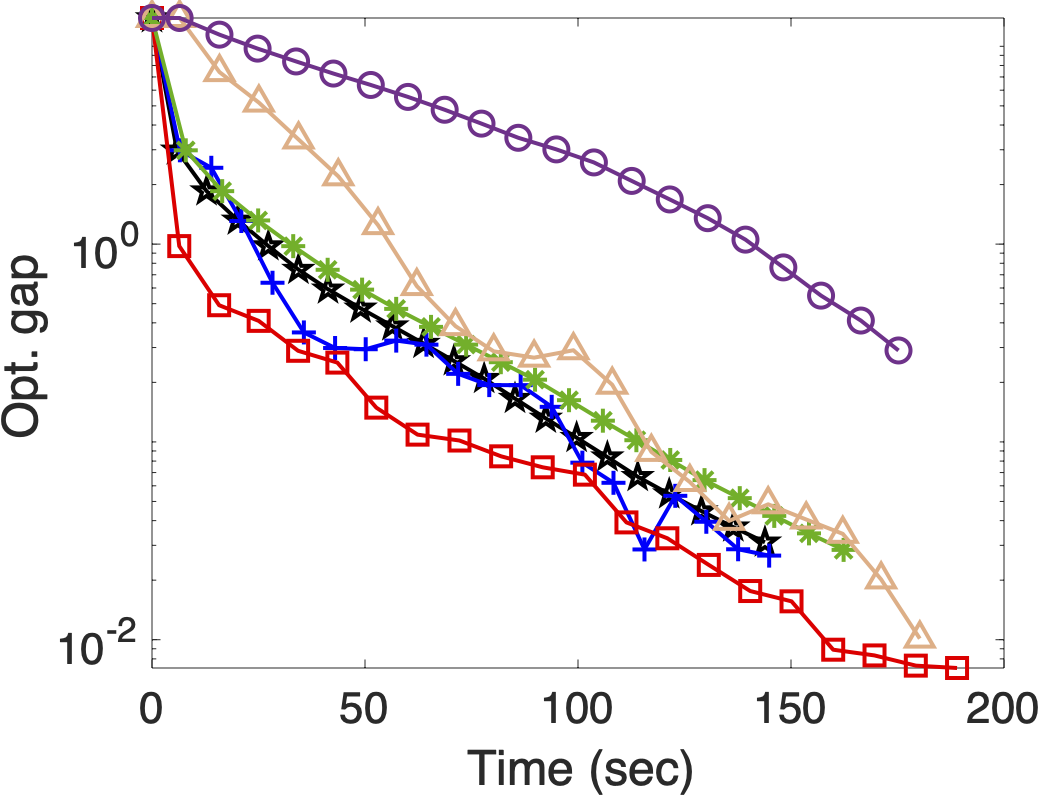
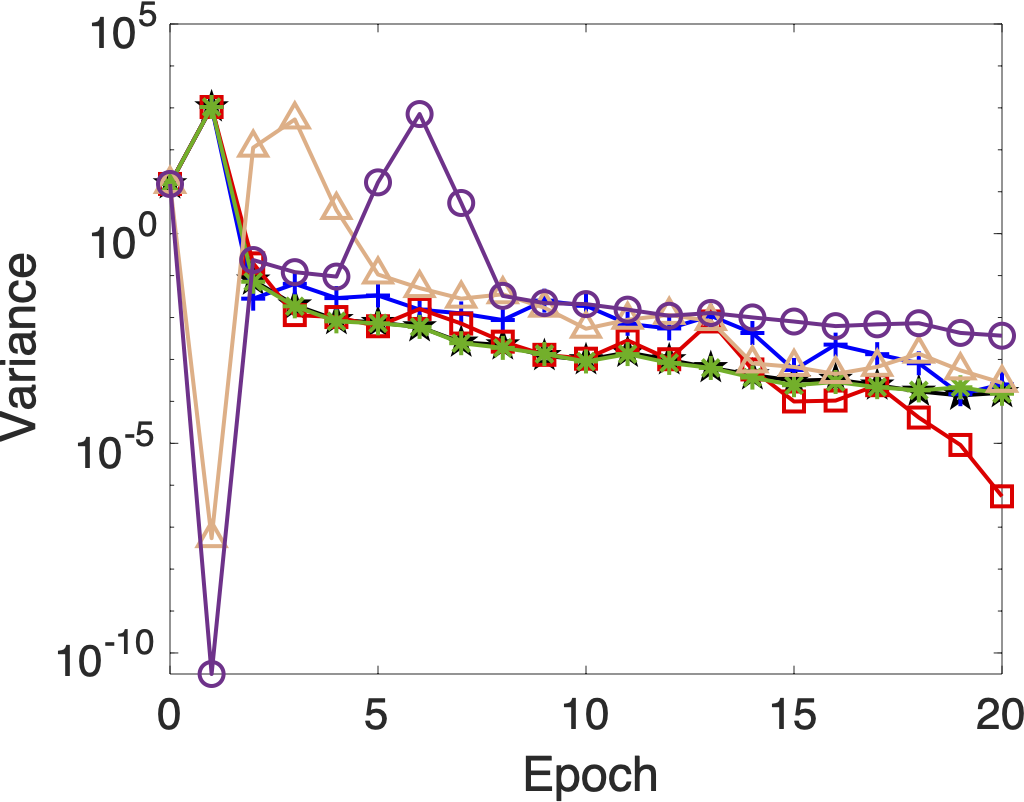
📊 Performance on Gisette Dataset

The Gisette dataset is a high-dimensional binary classification problem used to benchmark performance.

Key Metrics:

Gisette dataset: \#n : 6000 , \#d: 5001 and $\lambda = 1e-5$

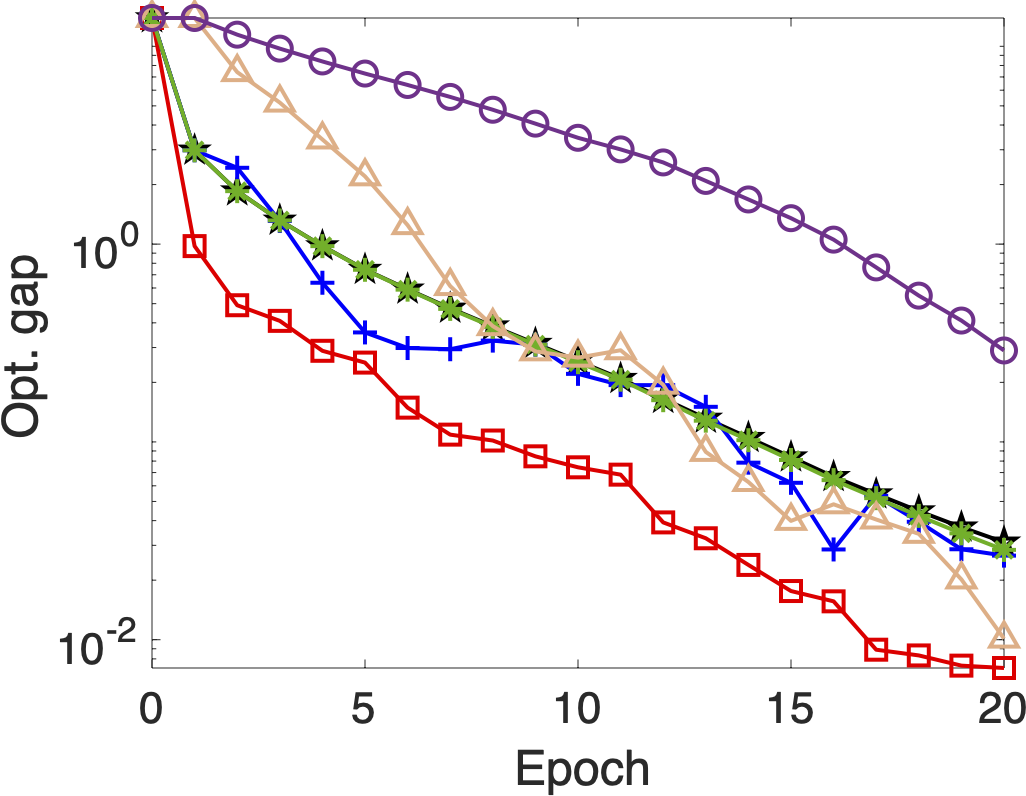
🔄 Optimality Gap vs. Epoch: Shows how quickly the algorithm nears the optimal solution. One can note that SVRG2BB outperforms other existing methods.
⏱ Optimality Gap vs. CPU Time: Demonstrates real-world training efficiency.
🔁 Variance vs. Epoch: Illustrates how SVRG2BB effectively reduces stochastic gradient noise.

📌 Use Cases

Optimization Research: MATLAB framework for experimenting with SVRG enhancements.
Benchmarking Solvers: Evaluate convex optimization algorithms.
Large-Scale ML Applications: Efficiently train models with high data volumes.
Educational Tool: Demonstrate and understand variance-reduction and step-size adaptation techniques.

You can explore and run all experiments from this GitHub repo. It provides a clean MATLAB setup for testing various SVRG variants, including the proposed Barzilai-Borwein approximations, allowing you to reproduce and experiment with these powerful optimization techniques.

📄 Citation

Tankaria, H., & Yamashita, N.
A Stochastic Variance Reduced Technique using Barzilai-Borwein techniques as second order information.
Journal of Optimization, Industry, and Management, 2024, 20(2): 525-547
DOI Link

📬 Contact

For questions or collaborations, reach out:

📧 hardiktankaria1406@gmail.com